三角関数で図形をまるく配置してみよう
円形に図形を配置することを考えてみよう。キャンプファイヤーを囲む人、ヒマワリの花びら、ホールケーキの苺…。ほかにもいろいろありそうです。
円形に図形を並べるのって、どうしたらいいんでしょう?
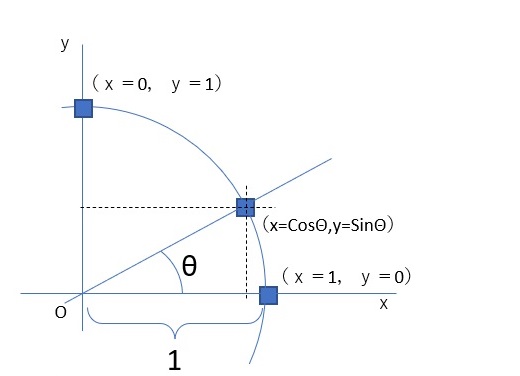
とりあえず、原点(0,0)を通る半径1の円を考えましょうか。x軸との交点は、(1,0)と(-1,0)ですね。同じように、y軸との交点は(0,1)と(0,-1)であることがわかります。
そのほかの点は…、ちょっと計算では難しそうですね。
中心角を決めた時に、x座標とy座標がわかればよさそうなのですが…。
昔の人は、ちゃんと答えを用意してくれています。それが、「三角関数」です。
中心角をθとしたときのx座標をcosθと表します。同じく中心角θのy座標はsinθです。
むずかしいですか?今は理解できなくても大丈夫。こんなふうに書くって、昔の人が決めたんだ、て思っておきましょう。
ところで、上の図、数学では一般的な表現なのですが、、縦のy軸は原点O(オー)を0として、上に行くほど大きくなります。エクセルでは、左上が0で下に行くほど大きくなるので、注意が必要です。
とりあえず3点ほど書いてみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Sub 円形に配置() Dim pi As Double pi = 3.14159 Dim Ox As Double Dim Oy As Double Dim r As Double Dim x As Double Dim y As Double Dim th As Double Dim t As Long Ox = 200 Oy = 200 r = 100 For t = 0 To 2 th = (t * 30) * pi / 180 x = Ox + Cos(th) * r y = Oy + Sin(th) * r Shapes.AddShape msoShapeRectangle, x, y, 10, 10 Next t End Sub |
わぉ!一気に複雑になってきました。でも、ゆっくり読み解けば大丈夫です!
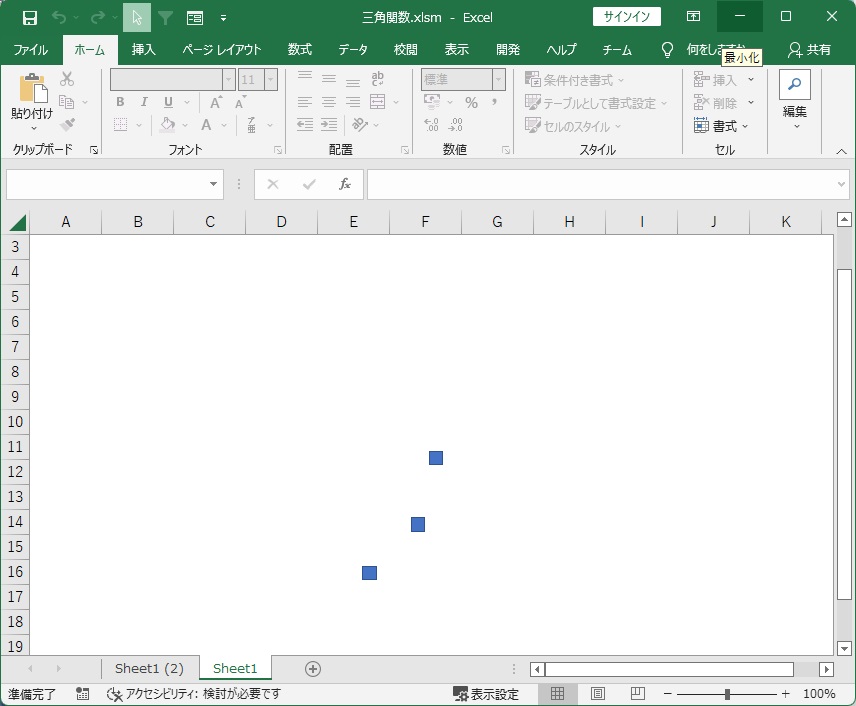
ほらね。y座標がさっきの説明図と違って、下へ伸びてますね。y座標が下が大なので、こうなっちゃうんです。が、今回は、特に問題ないのでよしとします。
さて、プログラムの説明です。
Dim pi As Double
pi = 3.14159とりあえず、円周率を定義しておきましょう。ギリシャ文字πを使いたいところですが、ちょっといろいろ面倒なので、アルファベットでpiとしておきます。doubleというのは小数型の変数の宣言です。
Dim Ox As Double
Dim Oy As Double
Dim r As Doubleエクセルでは画面左上角が原点(0,0)になります。三角関数では、円の中心が原点になるので、円全体を表示するためには、円の中心を少し右下にずらしたいですよね。
なので、右にOx、下にOyだけ円の中心をずらします。
円の半径はrです。
プログラミングでは、角度はラジアンを使います。
度からラジアンに変換する公式は、
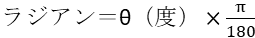
です。
For t = 0 To 2
th = (t * 30) * pi / 180
x = Ox + Cos(th) * r
y = Oy + Sin(th) * r
Shapes.AddShape msoShapeRectangle, x, y, 10, 10
Next t
では、tが1増えるごとに、thが30度ずつふえてますね。これもほんとはθと書きたいんですが、thとアルファベットで書いています。
それぞれのθにおけるx座標とy座標を計算して、幅10,高さ10の長方形を描いてます。
なんとなくわかりますか?
最後に、For t = 0 To 2のところをFor t = 0 To 11にかえて、全部の点を描いてみましょう。
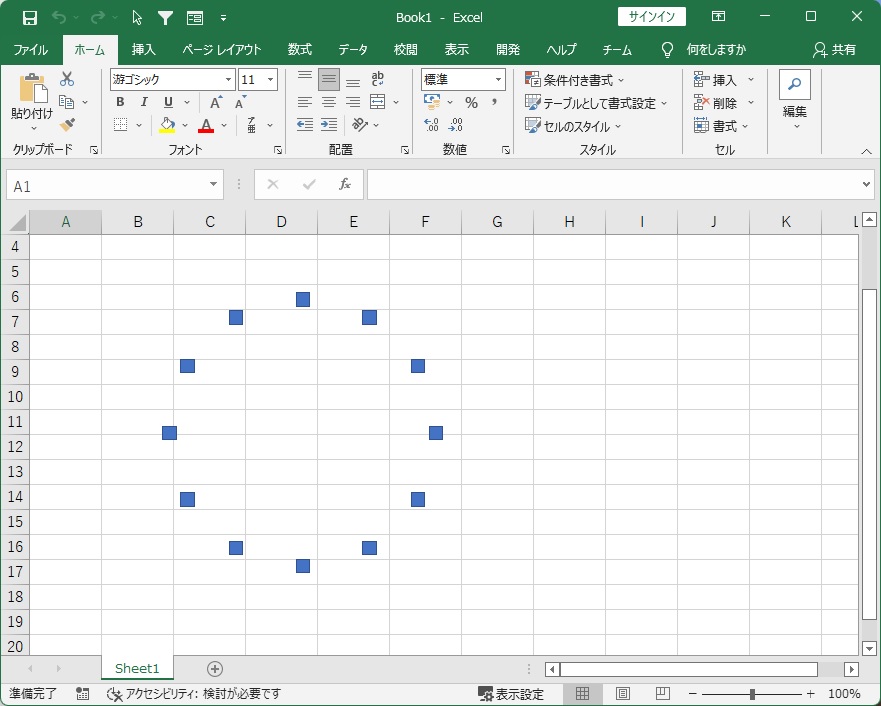
きれいに12個の四角形が円形に配置されました。


